1. 背景
前一段时间公司上线了一套Go实现的推荐系统,上线后发现MMR层虽然只有纯计算但耗时十分离谱,通过pprof定位问题所在之后进行了优化,虽然降低了非常多但是我们认为其中还有优化空间。

可以看到日常平均耗时126ms,P95 360ms。
MMR层主要耗时集中在了余弦相似度的计算部分,这部分我们使用的gonum库进行计算,其底层在x86平台上利用了SSE指令集进行了加速。
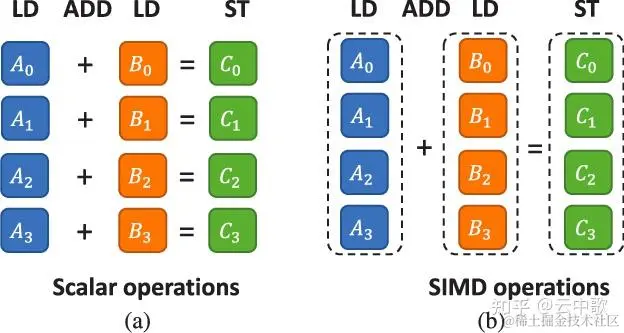
SSE指令集已经非常古老了,xmm寄存器只能存储两个双精度浮点数,每次只能并行进行两个双精度浮点数的计算,而AVX2指令集可以并行计算四个,理论上可以获得两倍的性能提升,因此我们决定自己使用AVX2指令集手写汇编的方式替代掉gonum库。
1.1 余弦相似度算法
余弦相似度的计算公式为

对应的代码为
import "gonum.org/v1/gonum/floats"
func CosineSimilarity(a, b []float64) float64 {
dotProduct := floats.Dot(a, b) // 计算a和b的点积
normA := floats.Norm(a, 2) // 计算向量a的L2范数
normB := floats.Norm(b, 2) // 计算向量b的L2范数
return dotProduct / (normA * normB)
}
2. Dot点积计算加速
gonum点积计算Dot的部分汇编代码如下:
TEXT ·DotUnitary(SB), NOSPLIT, $0
...
loop_uni:
// sum += x[i] * y[i] unrolled 4x.
MOVUPD 0(R8)(SI*8), X0
MOVUPD 0(R9)(SI*8), X1
MOVUPD 16(R8)(SI*8), X2
MOVUPD 16(R9)(SI*8), X3
MULPD X1, X0
MULPD X3, X2
ADDPD X0, X7
ADDPD X2, X8
ADDQ $4, SI // i += 4
SUBQ $4, DI // n -= 4
JGE loop_uni // if n >= 0 goto loop_uni
...
end_uni:
ADDPD X8, X7
MOVSD X7, X0
UNPCKHPD X7, X7
ADDSD X0, X7
MOVSD X7, sum+48(FP) // Return final sum.
RET
可以看到其中使用xmm寄存器并行计算两个双精度浮点数,并且还采用了循环展开的优化手段,一个循环中同时进行4个元素的计算。
我们利用AVX2指令集并行计算四个双精度浮点数进行加速
loop_uni:
// sum += x[i] * y[i] unrolled 8x.
VMOVUPD 0(R8)(SI*8), Y0 // Y0 = x[i:i+4]
VMOVUPD 0(R9)(SI*8), Y1 // Y1 = y[i:i+4]
VMOVUPD 32(R8)(SI*8), Y2 // Y2 = x[i+4:i+8]
VMOVUPD 32(R9)(SI*8), Y3 // Y3 = x[i+4:i+8]
VMOVUPD 64(R8)(SI*8), Y4 // Y4 = x[i+8:i+12]
VMOVUPD 64(R9)(SI*8), Y5 // Y5 = y[i+8:i+12]
VMOVUPD 96(R8)(SI*8), Y6 // Y6 = x[i+12:i+16]
VMOVUPD 96(R9)(SI*8), Y7 // Y7 = x[i+12:i+16]
VFMADD231PD Y0, Y1, Y8 // Y8 = Y0 * Y1 + Y8
VFMADD231PD Y2, Y3, Y9
VFMADD231PD Y4, Y5, Y10
VFMADD231PD Y6, Y7, Y11
ADDQ $16, SI // i += 16
CMPQ DI, SI
JG loop_uni // if len(x) > i goto loop_uni
可以看到我们每个循环中同时用到8个ymm寄存器即一次循环计算16个数,而且还用到了VFMADD231PD指令同时进行乘法累积的计算。
最终Benchmark结果:
BenchmarkDot 一个循环中计算8个数
BenchmarkDot-2 14994770 78.85 ns/op
BenchmarkDot16 一个循环中计算16个数
BenchmarkDot16-2 22867993 53.46 ns/op
BenchmarkGonumDot Gonum点积计算
BenchmarkGonumDot-2 8264486 144.4 ns/op
可以看到点积部分我们得到了大约2.7倍的性能提升
3. L2范数计算加速
gonum库中进行L2范数计算的算法并不是常规的a1^2 + a2^2 ... + aN^2这种计算,而是采用了Netlib算法,减少了溢出和下溢,其Go源码如下:
func L2NormUnitary(x []float64) (norm float64) {
var scale float64
sumSquares := 1.0
for _, v := range x {
if v == 0 {
continue
}
absxi := math.Abs(v)
if math.IsNaN(absxi) {
return math.NaN()
}
if scale < absxi {
s := scale / absxi
sumSquares = 1 + sumSquares*s*s
scale = absxi
} else {
s := absxi / scale
sumSquares += s * s
}
}
if math.IsInf(scale, 1) {
return math.Inf(1)
}
return scale * math.Sqrt(sumSquares)
}
其汇编代码比较晦涩难懂,但管中窥豹再结合Go源码可以看出来没有用到并行能力,每次循环只计算一个数
TEXT ·L2NormUnitary(SB), NOSPLIT, $0
...
loop:
MOVSD (X_)(IDX*8), ABSX // absxi = x[i]
...
我们优化之后的核心代码如下:
loop:
VMOVUPD 0(R8)(SI*8), Y0 // Y0 = x[i:i+4]
VMOVUPD 32(R8)(SI*8), Y1 // Y1 = y[i+4:i+8]
VMOVUPD 64(R8)(SI*8), Y2 // Y2 = x[i+8:i+12]
VMOVUPD 96(R8)(SI*8), Y3 // Y3 = x[i+12:i+16]
VMOVUPD 128(R8)(SI*8), Y4 // Y4 = x[i+16:i+20]
VMOVUPD 160(R8)(SI*8), Y5 // Y5 = y[i+20:i+24]
VMOVUPD 192(R8)(SI*8), Y6 // Y6 = x[i+24:i+28]
VMOVUPD 224(R8)(SI*8), Y7 // Y7 = x[i+28:i+32]
VFMADD231PD Y0, Y0, Y8 // Y8 = Y0 * Y0 + Y8
VFMADD231PD Y1, Y1, Y9
VFMADD231PD Y2, Y2, Y10
VFMADD231PD Y3, Y3, Y11
VFMADD231PD Y4, Y4, Y12
VFMADD231PD Y5, Y5, Y13
VFMADD231PD Y6, Y6, Y14
VFMADD231PD Y7, Y7, Y15
ADDQ $32, SI // i += 32
CMPQ DI, SI
JG loop // if len(x) > i goto loop
我们采用原始的算法计算以利用到并行计算的能力,并且循环展开,一次循环中同时计算32个数,最终Benchmark结果:
BenchmarkAVX2L2Norm
BenchmarkAVX2L2Norm-2 29381442 40.99 ns/op
BenchmarkGonumL2Norm
BenchmarkGonumL2Norm-2 1822386 659.4 ns/op
可以看到得到了大约16倍的性能提升
4. 总结
通过这次优化我们在余弦相似度计算部分最终得到了(144.4 + 659.4 * 2) / (53.46 + 40.99 * 2) = 10.8倍的性能提升,效果还是非常显著的。相较于《记一次SIMD指令优化计算的失败经历》这次失败的初次尝试,本次还是非常成功的,切实感受到了SIMD的威力。
另外在本次优化过程中也涨了不少姿势
AVX-512指令降频问题
AVX-512指令因为并行度更高理论上性能也更高,但AVX-512指令会造成CPU降频,因此业界使用非常慎重,这一点可以参考字节的json解析库sonic的这个issue: https://github.com/bytedance/sonic/issues/319
循环展开优化
在一次循环中做更多的工作,优点有很多:
- 减少循环控制的开销,循环变量的更新和条件判断次数更少,降低了分支预测失败的可能性
- 增加指令并行性,更多的指令可以在流水线中并行执行
但一次循环使用过多的寄存器从实际Benchmark看性能确实更好,但是否存在隐患我没有看到相关的资料,希望这方面的专家可以指教一下。





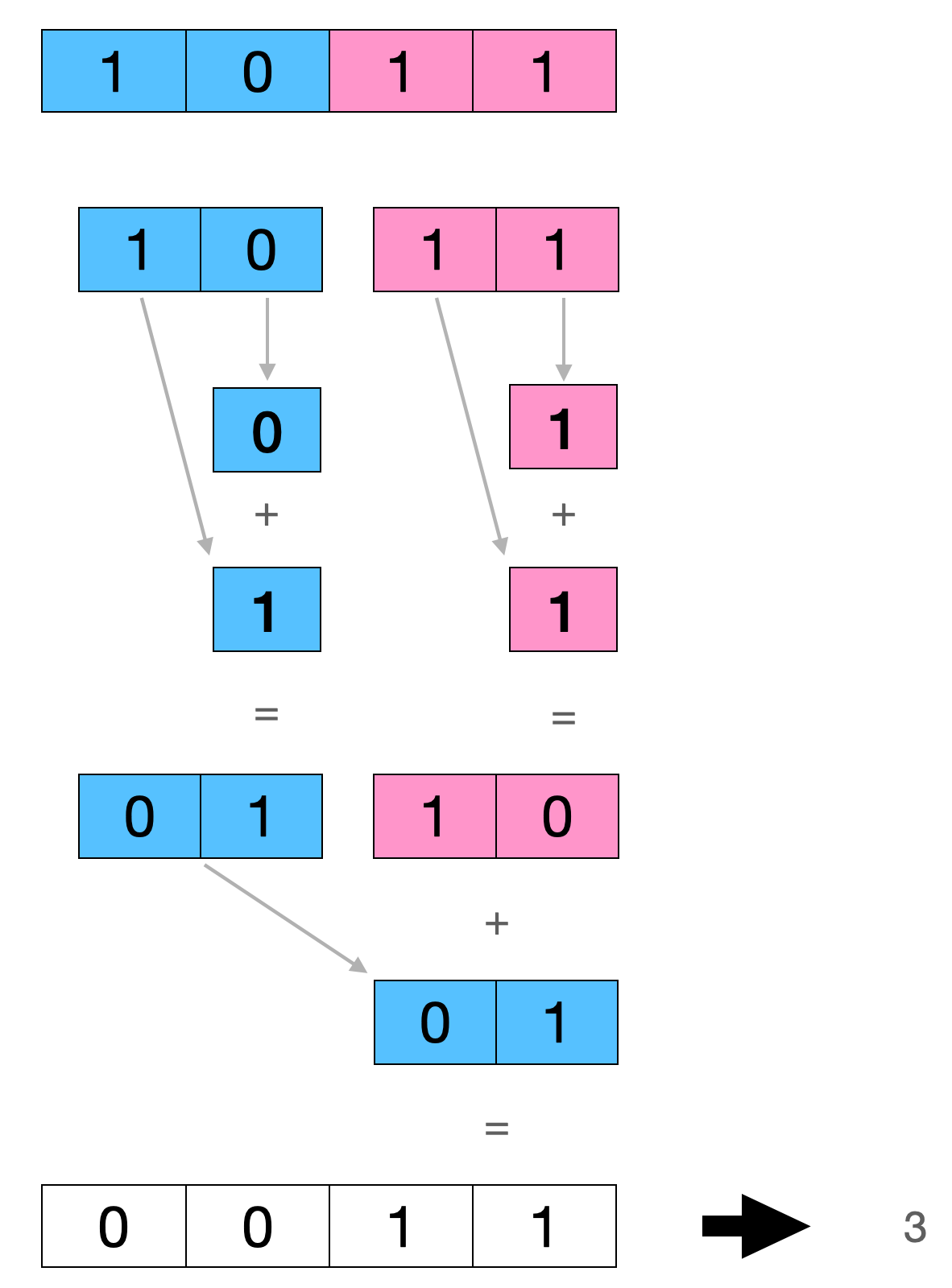

 继续往下看:
继续往下看: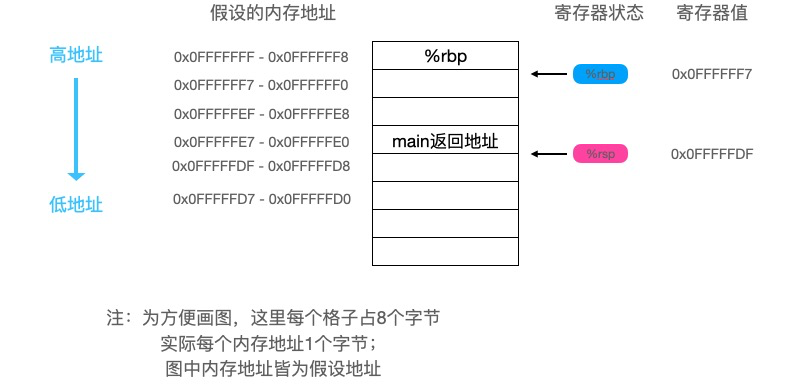
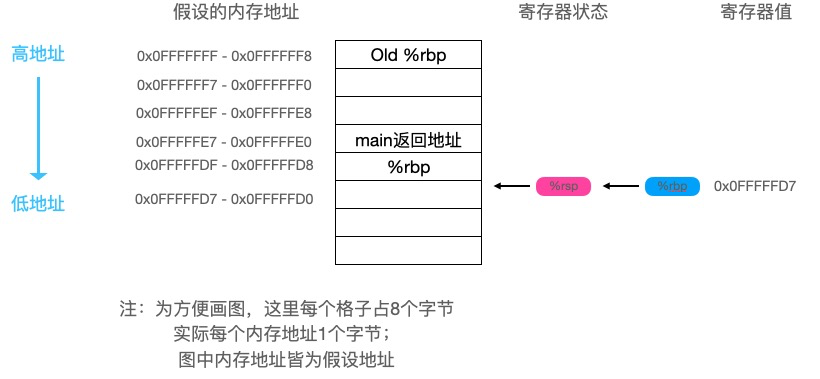
 foo函数最后执行了以下两条指令:
foo函数最后执行了以下两条指令: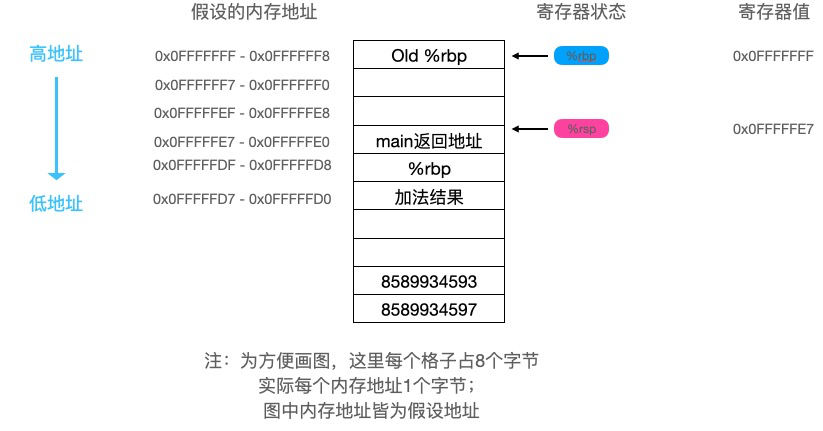

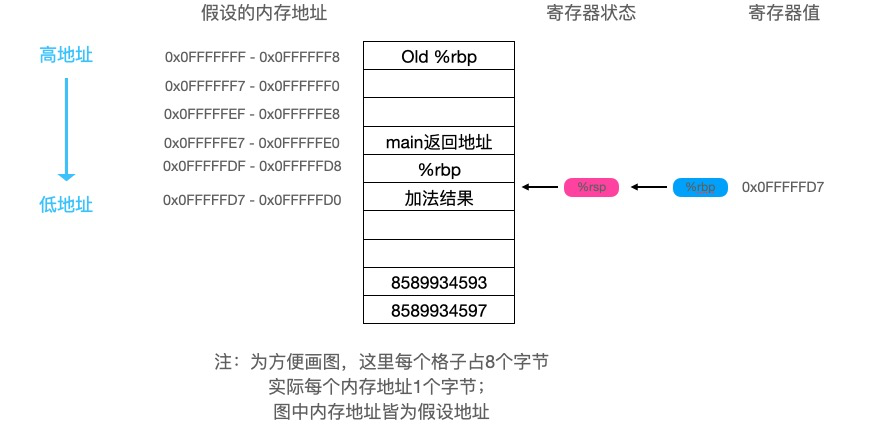
 可以看到a的值被存入了寄存器
可以看到a的值被存入了寄存器 可以看到eax寄存器中保存的值是
可以看到eax寄存器中保存的值是


 运行时,第一次循环中,CPU需要先加载x[0],由于高速缓存中一开始并没有,所以会从主存中加载x[0]-x[3]共16个字节(数据块的大小)的数据到高速缓存的
运行时,第一次循环中,CPU需要先加载x[0],由于高速缓存中一开始并没有,所以会从主存中加载x[0]-x[3]共16个字节(数据块的大小)的数据到高速缓存的
 可以看到我们只在结构体中加入了一个64字节的元素性能就得到了极大的提高,这是为什么呢?
可以看到我们只在结构体中加入了一个64字节的元素性能就得到了极大的提高,这是为什么呢? 之所以这样设计是基于电路工作效率考虑,这样的设计可以并行取8个字节的数据,如果想取址0x0000-0x0007,每个bank只需要工作一次就可以取到,IO效率比较高,如果这8个字节在同一个bank上则需要串行读取该bank8次才能取到。
之所以这样设计是基于电路工作效率考虑,这样的设计可以并行取8个字节的数据,如果想取址0x0000-0x0007,每个bank只需要工作一次就可以取到,IO效率比较高,如果这8个字节在同一个bank上则需要串行读取该bank8次才能取到。 总共占用13个字节。我们可以看到
总共占用13个字节。我们可以看到  总共占用20个字节,
总共占用20个字节, 这时总共占用16个字节,相比较上面我们节省了8个字节。
写段代码验证下:
这时总共占用16个字节,相比较上面我们节省了8个字节。
写段代码验证下:






