最近一个需求需要使用golang实现一个兼容redis的无压缩的bitmap，需要提供一个bitcoun函数来统计这个bitmap中二进制位1的个数，查了一圈并没有找到类似的第三方库，因此决定自己实现一个.（利用一切机会造轮子

1. 问题简化

问题本质实际就是给定一个数字，比如一个二进制数10101101，计算出这个数字中二进制位1的个数，对于10101101这个数字来说它有5个位为1，即：10101101

对于这个问题，最简单的办法就是挨位数，不过这个办法太笨了，没有逼格。

那么有没有银弹呢？答案是肯定的，而且还不止一种。

2. 查表法

对于一个8位的数字来说，它只有256个值，因此完全可以预先计算好每个值的二进制位1个个数写入到映射表中，使用时直接查询这张映射表即可。

伪代码如下所示：

var count1map = map[uint8]uint8 {
    0b0000_0000: 0,
    0b0000_0001: 1,
    ...
    0b1111_1111: 8,
}

func bitcount(x uint8) uint8 {
    return count1map[x]
}

3. 移位法

查表法虽然可以应对8位这样值数量有限的数字，但是对于uint64 or int64这样64位的数字来说，它的值数量是非常多的，我们无法在内存中维护这样巨大的映射表，因此不能使用查表法来解决

Golang在bits包中提供一个OnesCount64(x uint64) int的函数，可以计算一个64位数字中二进制为1的个数，其源码如下：

const m0 = 0x5555555555555555 // 01010101 ...
const m1 = 0x3333333333333333 // 00110011 ...
const m2 = 0x0f0f0f0f0f0f0f0f // 00001111 ...
const m3 = 0x00ff00ff00ff00ff // etc.
const m4 = 0x0000ffff0000ffff

func OnesCount64(x uint64) int {
	const m = 1<<64 - 1
	x = x>>1&(m0&m) + x&(m0&m)
	x = x>>2&(m1&m) + x&(m1&m)
	x = (x>>4 + x) & (m2 & m)
	x += x >> 8
	x += x >> 16
	x += x >> 32
	return int(x) & (1<<7 - 1)
}

初看起来是有点懵逼的，一顿位运算操作怎么就能把1的个数算出来了呢？

这段代码注释中标明其来源于Hacker’s Delight第5章

别着急，我们还是采用自底向上的思想来拆解下。

3.1 2位数字二进制位1的个数

我们先想一下如何计算2位的数字二进制位1的个数，答案是非常简单的：

func OnesCount2(x uint2) int {
    return (x & 0b01) + ((x >> 1) & 0b01)
}

x & 0b01就是求第0位是不是1，((x >> 1) & 0b01)就是求第1位是不是1，加起来就是x这个2位数字二进制位1的个数。

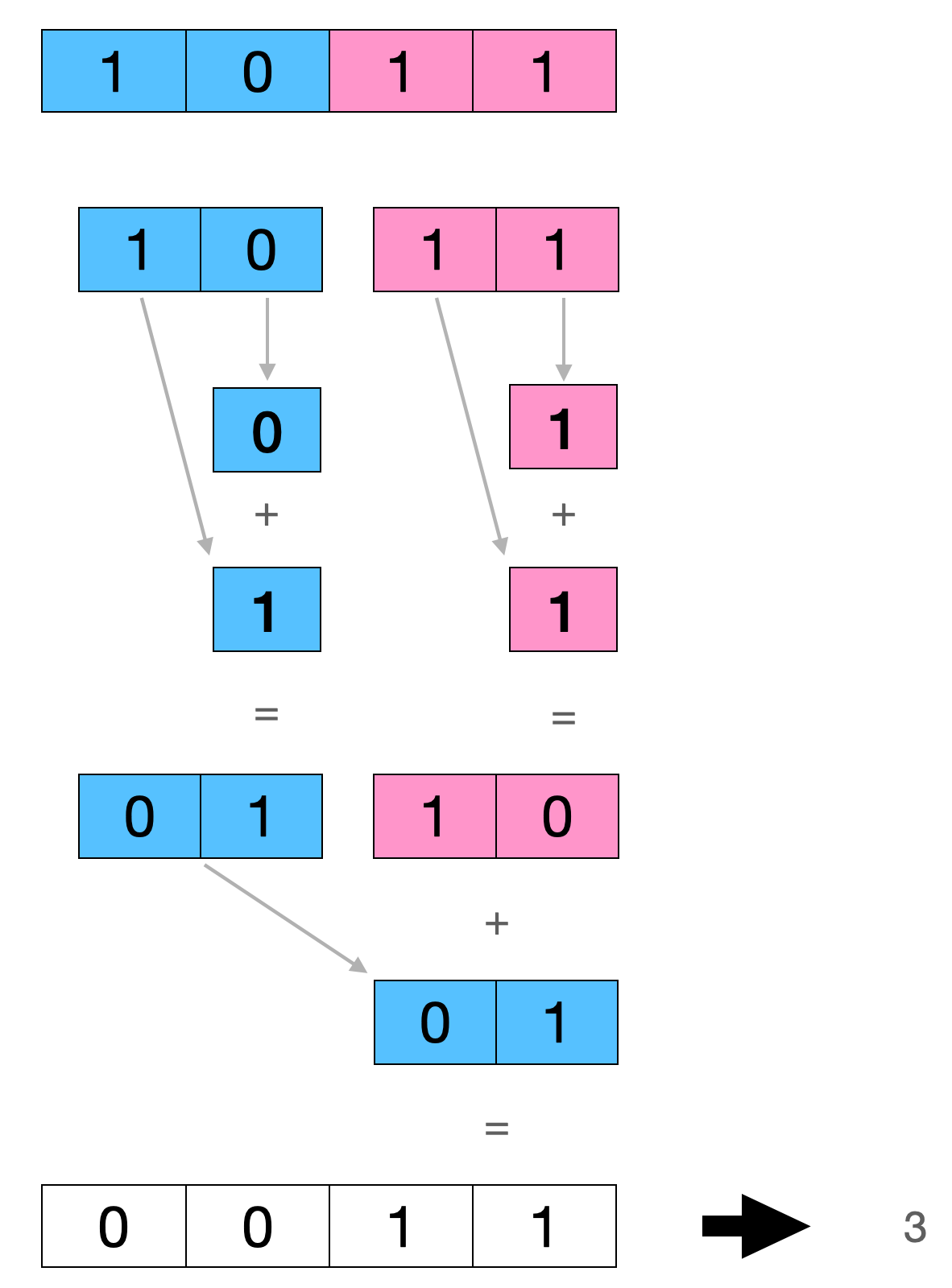
3.2 4位数字二进制位1的个数

对于一个4位数字，如1011，我们先按照3.1中的算法分别求出第3位与第2位即10 和 第1位与第0位即11的二进制位1的个数，然后再加起来就得出这个4位数字的二进制位1的个数了。

伪代码如下所示：

func OnesCount4(x uint4) int {
    x = x & 0b0101 + x >> 1 & 0b0101
    return x & 0b0011 + x >> 2 & 0b0011
}

计算过程如图：

3.3 8位数字二进制位1的个数

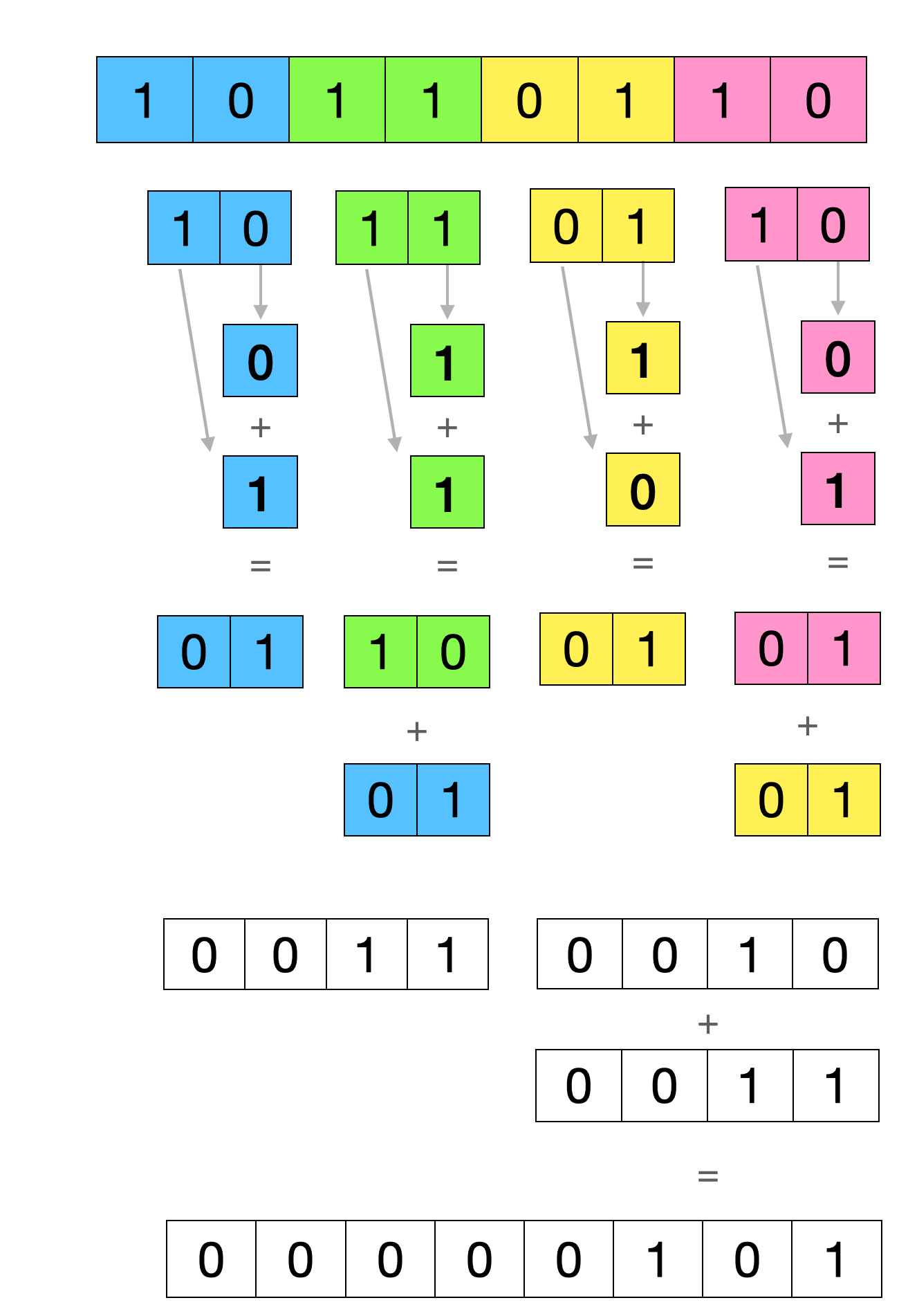
8位数字计算过程与4位计算过程本质是相同的，都是拆解组合，伪代码如下：

func OnesCount8(x uint8) int {
    x = x & 0b01010101 + x >> 1 & 0b01010101
    x = x & 0b00110011 + x >> 2 & 0b00110011
    return x & 0b00001111 + x >> 4 && 0b00001111
}

计算过程如下：

64位数字重复这个过程即可，回头看golang的代码应该就可以看懂了，这里就不再详细解释了。

另外这个算法过程还可以进一步优化，详细可以参考下：计算汉明权重的SWAR（SIMD within a Register）算法 感兴趣的可以研究一下，这里就不赘述了。

4. POPCNT指令

一些较新的CPU上支持POPCNT指令，可以通过硬件直接进行计算，Golang代码示例如下：

main.go文件

package main

import (
    "fmt"
    "math/bits"
    "math/rand"
    "time"
)

func main() {
    rand.Seed(time.Now().Unix())
    for i := 0; i < 100; i++ {
        var num = rand.Uint64()
        if popcnt(num) != bits.OnesCount64(num) {

            panic(fmt.Sprintf("i: %d, popcnt(%b) = %d, bits.OnesCount64(%b) = %d", i, num, popcnt(num), num, bits.OnesCount64(num)))
        }
    }
    fmt.Println("ok")
}

func popcnt(x uint64) int

amd64.s 文件

#include "textflag.h"

TEXT main·popcnt(SB), NOSPLIT, $0-8
    MOVQ x+0(FP), AX // 将参数x移到AX寄存器
    BYTE $0xf3; BYTE $0x48; BYTE $0x0f; BYTE $0xb8; BYTE $0xc0  // 计算二进制X中1的个数，golang编译器不支持POPCNT指令，这行对应于POPCNT AX, AX
    MOVQ AX, ret+8(FP) // 将结果存入ret
    RET