1. 简介
最近在学习rust,恰好看到了skywalking的php扩展采用了rust编写。有用过Skywalking/CAT之类监控系统的同学应该知道,这类系统对我们开发工作帮助非常大,能够非常快的帮我们定位到问题的关键,比如说现在有一个api的请求响应非常慢,那我们就可以从系统提供的web ui中查询这个api请求的链路各个节点的耗时,从而精准的定位慢的关键。
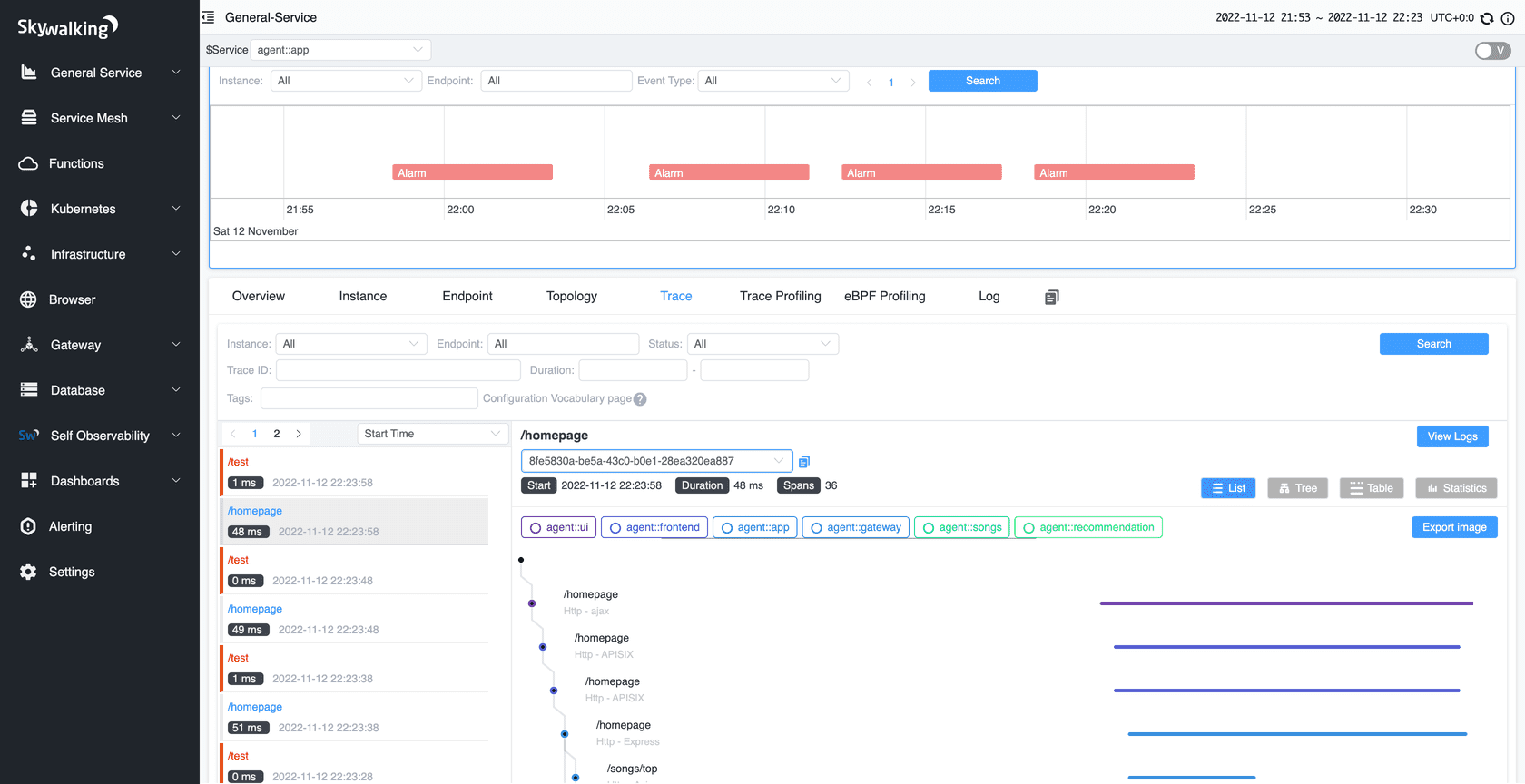
但是这类系统搭建起来还是比较繁琐的,对于个人开发者或者一些小公司来说成本比较高,因此我在apache/skywalking-php的基础上对其进行精简和部分增强,去掉其上报到skywalking server的部分,将trace log写入到本地文件,在这个本地文件中会记录以下内容:
1. 调用CURL时,记录开始结束时间以及耗时,如果发生错误会将错误信息记录下来
{
"trace_id": "b89143d7-0fda-43d5-a688-397aef0ee3ef",
"kind": "CURL",
"name": "https://error.blog.fanscore.cn/a/57/",
"payload": {
"http_code": "0",
"query": "k1=v1&k2=k2&k3=v3",
"curl_error": "Could not resolve host: error.blog.fanscore.cn"
},
"start_time": "10:19:03.596", // 时间格式%H:%M:%S%.3f
"end_time": "10:19:03.602",
"duration_in_micro": 5988 // 耗时
}
{
"trace_id": "b89143d7-0fda-43d5-a688-397aef0ee3ef",
"kind": "CURL",
"name": "https://blog.fanscore.cn/a/57/",
"payload": {
"http_code": "200",
"curl_error": "",
"query": "k1=v1&k2=k2&k3=v3"
},
"start_time": "10:19:03.602",
"end_time": "10:19:03.969",
"duration_in_micro": 366647
}
2. 调用PDO函数时,记录开始结束时间以及耗时,如果发生错误会将错误信息记录下来
{
"trace_id": "b89143d7-0fda-43d5-a688-397aef0ee3ef",
"kind": "PDO",
"name": "__construct",
"payload": {
"result": "unknown",
"dsn": "mysql:host=127.0.0.1;dbname=blog;charset=utf8mb4"
},
"start_time": "10:19:03.969",
"end_time": "10:19:03.980",
"duration_in_micro": 11175
}
{
"trace_id": "b89143d7-0fda-43d5-a688-397aef0ee3ef",
"kind": "PDO",
"name": "query",
"payload": {
"statement": "select * from article",
"result": "object(PDOStatement)"
},
"start_time": "10:19:03.980",
"end_time": "10:19:03.985",
"duration_in_micro": 5471
}
{
"trace_id": "b89143d7-0fda-43d5-a688-397aef0ee3ef",
"kind": "PDO_STATEMENT",
"name": "fetchAll",
"payload": {
"query_string": "select * from article",
"result": "array(3)"
},
"start_time": "10:19:03.985",
"end_time": "10:19:03.985",
"duration_in_micro": 25
}
3. 捕获PHP代码中的错误
{
"trace_id": "b89143d7-0fda-43d5-a688-397aef0ee3ef",
"kind": "ERROR",
"name": "E_WARNING: Undefined variable $undefined_value in /Users/orlion/workspace/nginx/www/ptrace/index.php on line 32",
"payload": {},
"start_time": "10:19:03.986",
"end_time": "10:19:03.986",
"duration_in_micro": 2
}
4. 捕获PHP代码中未捕获的异常
{
"trace_id": "b89143d7-0fda-43d5-a688-397aef0ee3ef",
"kind": "EXCEPTION",
"name": "Exception: test exception in /Users/orlion/workspace/nginx/www/ptrace/index.php on line 34",
"payload": {
"trace": "#0 {main}"
},
"start_time": "10:19:03.986",
"end_time": "10:19:03.986",
"duration_in_micro": 1
}
5. 请求结束后会记录请求开始结束时间、状态码、GET/POST参数
{
"trace_id": "b89143d7-0fda-43d5-a688-397aef0ee3ef",
"kind": "URL",
"name": "/index.php",
"payload": {
"$_GET": "{\"a\":\"1\",\"b\":\"2\",\"c\":\"3\"}",
"$_POST": "[]",
"method": "GET",
"status_code": "200"
},
"start_time": "10:19:03.595",
"end_time": "10:19:03.992",
"duration_in_micro": 397178
}
2. 安装
- Requirement
很遗憾,目前只提供mac arm64版本,后续会编译出linux版本,但因为依赖的phper-framework/phper的库不支持windows,因此短期内恐怕不能提供windows版本了。
-
进入https://github.com/Orlion/minitrace/releases 下载编译好的扩展二进制文件到本地
-
假设第一步将扩展下载到了/tmp/minitrace-v0.1.0-macos-arm64.dylib,编辑php.ini配置文件加入以下配置
[minitrace]
;加载我们的扩展
extension=/tmp/minitrace-v0.1.0-macos-arm64.dylib
;将trace数据输出到/tmp/minitrace.log
minitrace.log_file = /tmp/minitrace.log
- 重启fpm
3. 测试使用
编辑以下php文件
<?php
$ch = curl_init();
curl_setopt($ch, CURLOPT_URL, 'https://error.blog.fanscore.cn/a/57/?k1=v1&k2=k2&k3=v3#aaa');
curl_setopt($ch, CURLOPT_RETURNTRANSFER, true);
$response = curl_exec($ch);
$ch = curl_init();
curl_setopt($ch, CURLOPT_URL, 'https://blog.fanscore.cn/a/57/?k1=v1&k2=k2&k3=v3#aaa');
curl_setopt($ch, CURLOPT_RETURNTRANSFER, true);
$response = curl_exec($ch);
$host = '127.0.0.1';
$db = 'blog';
$user = 'root';
$pass = '123456';
$charset = 'utf8mb4';
$dsn = "mysql:host=$host;dbname=$db;charset=$charset";
$options = [
PDO::ATTR_ERRMODE => PDO::ERRMODE_EXCEPTION,
PDO::ATTR_DEFAULT_FETCH_MODE => PDO::FETCH_ASSOC,
PDO::ATTR_EMULATE_PREPARES => false,
];
$pdo = new PDO($dsn, $user, $pass, $options);
$stm = $pdo->query('select * from article');
$rows = $stm->fetchAll();
foreach($rows as $row) {
print_r($row);
}
var_dump($undefined_value);
throw new Exception('test exception');
?>
然后在浏览器中请求该文件,打开/tmp/minitrace.log就能看到如下输出:
{"trace_id":"b89143d7-0fda-43d5-a688-397aef0ee3ef","kind":"CURL","name":"https://error.blog.fanscore.cn/a/57/","payload":{"http_code":"0","query":"k1=v1&k2=k2&k3=v3","curl_error":"Could not resolve host: error.blog.fanscore.cn"},"start_time":"10:19:03.596","end_time":"10:19:03.602","duration_in_micro":5988}
{"trace_id":"b89143d7-0fda-43d5-a688-397aef0ee3ef","kind":"CURL","name":"https://blog.fanscore.cn/a/57/","payload":{"http_code":"200","curl_error":"","query":"k1=v1&k2=k2&k3=v3"},"start_time":"10:19:03.602","end_time":"10:19:03.969","duration_in_micro":366647}
{"trace_id":"b89143d7-0fda-43d5-a688-397aef0ee3ef","kind":"PDO","name":"__construct","payload":{"result":"unknown","dsn":"mysql:host=127.0.0.1;dbname=blog;charset=utf8mb4"},"start_time":"10:19:03.969","end_time":"10:19:03.980","duration_in_micro":11175}
{"trace_id":"b89143d7-0fda-43d5-a688-397aef0ee3ef","kind":"PDO","name":"query","payload":{"statement":"select * from article","result":"object(PDOStatement)"},"start_time":"10:19:03.980","end_time":"10:19:03.985","duration_in_micro":5471}
{"trace_id":"b89143d7-0fda-43d5-a688-397aef0ee3ef","kind":"PDO_STATEMENT","name":"fetchAll","payload":{"query_string":"select * from article","result":"array(3)"},"start_time":"10:19:03.985","end_time":"10:19:03.985","duration_in_micro":25}
{"trace_id":"b89143d7-0fda-43d5-a688-397aef0ee3ef","kind":"ERROR","name":"E_WARNING: Undefined variable $undefined_value in /Users/orlion/workspace/nginx/www/ptrace/index.php on line 32","payload":{},"start_time":"10:19:03.986","end_time":"10:19:03.986","duration_in_micro":2}
{"trace_id":"b89143d7-0fda-43d5-a688-397aef0ee3ef","kind":"EXCEPTION","name":"Exception: test exception in /Users/orlion/workspace/nginx/www/ptrace/index.php on line 34","payload":{"trace":"#0 {main}"},"start_time":"10:19:03.986","end_time":"10:19:03.986","duration_in_micro":1}
{"trace_id":"b89143d7-0fda-43d5-a688-397aef0ee3ef","kind":"URL","name":"/index.php","payload":{"$_GET":"{\"a\":\"1\",\"b\":\"2\",\"c\":\"3\"}","$_POST":"[]","method":"GET","status_code":"200"},"start_time":"10:19:03.595","end_time":"10:19:03.992","duration_in_micro":397178}
...